Quantum computers are much more efficient in solving computations than classical computers and we refer to this principle as quantum supremacy. We are all aware of the uniqueness of quantum mechanics in physics, how state collapses by measurement, and how particles are entangled with each other such that their states are dependent on one another. These properties are fundamental in quantum information and their applications are also very useful in the modern world. For instance, quantum cryptography is highly demanding when we want to encrypt any information. Similarly, we have error handling which secures the fidelity of communication in quantum. The study of using quantum mechanical laws in communication and information is basically quantum information (QI). In QI, we use the properties of particles such as entanglement, decoherence, and superposition to develop strategies or ideas for a better information and communication process. While classical information regulates classical physics and computation, quantum information deals with superposition and other quantum properties of particles.
When we deal with classical communication using regular bits in a computer, all the processes the computer retrieves are basically by the flow of electrons. If we want to operate a certain function in a computer, then it uses numerous electrons to operate that function. Hence the more complex the function, the more electrons it regulates. This is why some complex problems take a long time to operate in classical computers. In quantum computers, instead of using billions of electrons to operate tasks, they use a single electron making it extremely efficient. However, the problem with today's quantum computer is the error handling. If we only use one electron to perform any task, there is a high percentage of error in that electron since particles are extremely fragile under fields. For this reason, quantum error handling is becoming one of the most important research areas in QI.
If we can minimize the errors in quantum computers then we can solve complex functions at very few times compared to classical computers.
Quantum state
In classical physics, we describe almost everything with a state in a 3-dimensional vector space. If we have a car moving at some speed, it has its x,y, and z components under some period(t). This is what a classical state represents. In quantum mechanics, a quantum state is required such that the properties of the particles are described in 2D complex vector space. These 2D complex vector space representations are called "Hilbert Space". The representation of quantum states in complex vector space doesn't mean they are not real, in fact, they can also be represented in real space but the properties of particles tend to be different than in the classical world which makes it difficult to be represented under real vector space. To first understand a quantum state, we must deal with one of the prominent quantum properties in a particle, "superposition."
Superposition
A superposition is a property where the state can exist in multiple states at once. For example, a qubit(unit of QI) is a superposition of bits 0 and 1 that can exist at both bases at the same time. This means a qubit state is basically 0 bit and 1 bit simultaneously unless the measurement is applied. A superposition is a key feature in the quantum world that distinguishes particles from the classical world. Almost everything that is described by a quantum state has superposition in them. A superposition could be between spins, polarization, qubits, etc. Basically, a superposition is a certain feature in quantum such that we are uncertain about the outcome of the state (could be spin up or spin down) until and unless we make a measurement. This means that the cat is alive and dead simultaneously until we open the box and see the result.
How is superposition different from probability?
When I first learned about the superposition property, my first question was how is it different from classical probability? In other words, when we say that the cat is alive/dead at the same time (the cat's life is in superposition), how is it different from assuming the cat is 50% alive and 50% dead? The key difference here is such that when a certain property is measured on a superposition state, we get a definite result and that result will be the same for infinite times until we change the measurement basis (changing the axis from x to z). However, in classical probability, outcomes are completely uncertain. If we toss a coin and land heads first it doesn't mean that we will get heads every time we toss the coin. If instead of probability, we have superposition in the coin, we will get heads every time we flip the coin.
That being said, if a state is described with a probability of a mixture of other states, we can say that the state is more disturbed since the measurement done in the state will still be random. However, if a state is pure which means if it only has superposition then once a measurement is made, it will always be in the same state. This means that the entropy of the mixed state will always be greater than the entropy of the pure state since the mixed state is random whilst the pure state is dependent only on measurement.

This equation is the most general equation representing a state in quantum mechanics. The psi, 0, and 1 are inside a weird bracket called the "Ket". The symbol ket represents that the state is pure.
In this equation, the psi (state) is such that it is a linear combination of the qubits 0 and 1. The coefficients alpha and beta are a complex number that represents the probability of measuring the state in either basis states 0 or 1.
What is superposition?
Almost everyone interested in quantum mechanics has definitely heard of superposition. From Schrodinger's cat experiment, we see that the cat is both alive and dead at the same time. Superposition is an important part of quantum information that describes quantum magic. A superposition is something that always interests people to learn quantum. How can a cat be alive or dead at the same time, it violates classical physics!
In quantum, a superposition is something that exists in a phase such that it is probabilistic and collapses after the measurement. In the first equation, we see that the state psi is in a superposition of either qubit 0 or qubit 1. This means before measuring the state psi, it is in such a super phase where there is no certainty of the specific information which is what qubit it holds. But if we measure the system then the superposition property collapses and then we get a finite state which is qubit 0 or 1. So what are those complex numbers alpha and beta? Well, alpha and beta are basically the probability of the corresponding qubits. The modulus of alpha squared gives us the probability of finding the qubit 0 while the modulus of beta squared gives the probability of finding the qubit 1 after the measurement.
In other words, a quantum state is a linear combination of basis (in this case qubits) represented in a superposition with the probability that is the coefficient. This means that the sum of alpha squared and beta squared should always be 1.

Again the coefficients of the bases give us the probabilities of finding the corresponding basis.
Let's look at a specific example to understand

In this example, the psi is defined such that we have a superposition of qubits 0 and 1 with the corresponding probability of 4/5 for qubit 0 and 1/5 for qubit 1. This means if we measure this state then we have a higher chance of getting qubit 0 than 1 since the modulus square for the coefficient of qubit 0 is higher than for qubit 1.
What is the difference between probability and superposition?
When I was learning quantum information, I used to struggle a lot to find the difference between probability and superposition. Many get confused since probability acts very much like a superposition property. However, a key thing to remember is the number of sample spaces.
If we have a state in a superposition of spin up or spin down, then what it means is that after you measure that state and find it in state up, you will always get the same state to spin up until and unless you change your measurement basis.
To explain it more clearly, superposition is something that only depends upon the basis of measurement. If we measure a quantum state in the z-axis (let's say) and find a corresponding property under that axis then even if I measure it infinite times, I'll always get the same corresponding state until and unless I change my measurement basis to another axis (except from z). This means after the measurement the state is clearly defined.
However, in probability, the result is still random. If I have a 50% chance of getting a head from a coin with infinite trials, then I will get the number of tails and number of heads equal. To sum it up, a probability is something that can be changed depending on the number of trials and it is basically random but superposition is probabilistic before the measurement but remains fixed for any trials until the measurement axis is changed.
An analogy for this is if a cat is in a superposition of either alive or dead and when we open the box, the cat is dead according to your specific axis. Now even if you do this 1000 times with your same specific axis, you will find the cat dead in all of the cases. However, if this scenario is classical which only includes probability, in this case cat might be alive in 500 trials and dead in the other 500 trials.
This is the main difference between probability and superposition. They both act in the same way but they are different.
So what does it mean when we have a probability in the state equation. Why do we have alpha and beta? Well, they are basically probabilities of finding either qubit 0 or 1 (in the above figure), however, their linear combination is actually the superposition state.
The quantum state can be a superposition of many things such as spin, polarization, qubits, etc. Now that we understand about quantum state, we will try to comprehend the purity of quantum states. In other words, are there any differences within the states itself? Can we have a superposition between the states themselves instead of the basis? Can we have a double superosition where in one case you have psi_1 or psi_2 and when measured we have psi_1 but then again in that state, we have either spin up or spin down. Also, can we have a linear combination of multiple states that are associated with probabilities? If so, what are they called, and their significance in the quantum world?
In quantum mechanics, the states are defined with 3 purities:
1. Pure state
2. Mixed state
3. Maximally mixed state
To understand the properties of quantum states, we first must understand the key difference between these purities and how their unique properties play some key role in understanding quantum information. We will then represent the purity of the states in the Bloch sphere.
1. Pure State:
A pure state is the purest quantum state. The pure state and only the pure state can be represented by the ket vector described above. Basically, a pure ket state is something that is only a singular state meaning there is no mixture of probabilistic states. For example in this pure state:
we see that the psi is represented by the ket vector which means the state is pure. This means when we observe the state and collapse the wavefunction, we will only get either qubit 0 or qubit 1 but nothing outside of the state since it only has one state representing the entire state and its probability is always 100%. Think of pure state like a picture with high resolution and the picture is encoded with small accurate pixels that are from the picture. There is no outside blend of another picture, it is just one picture with 100% probability and the pixels are a superposition of the basis states that are only the component of the state psi but not others.
Properties of Pure state:
A general pure state can be represented as
Here we see that since there is only state psi represented under the ket vector, we call this the pure state. A pure state must have the following properties:
a. The eigenvalues of the pure state when represented by the density operator (we will cover in the next blog) should always be 1,0,0,...0.
b. The Trace(sum of the diagonals of the density) squared should always be equal to the Trace of the density of the pure state. ( Trace is idempotent)
The density operator is the other factor that needs to be discussed immediately. As of now, we will only discuss the states and the purity and we will explain the density operator in our later posts. Right now, think of the density operator as an inner product of the state with its complex conjugate which is represented in a matrix form.
2. Mixed state:
A mixed state is a probabilistic mixture of other pure states. Basically in a pure state, when we measure anything we get values within the pure state (since the eigenvalues are 0 and 1). In a mixed state, since it combines different states (psi), the outcome depends on the probability. If one pure state is psi_1 and the other pure state is psi_2 then a mixed state can be something like a state such that there is an 80% chance of psi_1 and a 20% chance of psi_2. This means if we measure the mixed state we are more likely to get psi_1 because of the higher probability. Hence a mixed state unlike a pure state depends both on superposition and probability of multiple states.
Since a mixed state is the combination of pure states, the sum of the probability of each pure state must be equal to 1.
As mixed states are not pure, we cannot represent these states with a ket vector. Instead, to represent a mixed state we need to use a special type of operator called the density operator. A density operator is a special power operator that describes the purity of the state. When dealing with calculations or any operations in QI, we highly use density operators since they define the mixed state. In our real-life world, many errors/noises tend to change a pure state into a mixed state which is why density operators are efficient in describing those states.
Since the ket operators can only represent the pure state, the density operator is a special operator that can map the state regardless of the purity of the states. A mixed state can be understood as something like this:
Here, the mixed state combines three pure states with their corresponding probabilities, p,q, and r. The first pure state (psi_1) has a probability of 'p', while the second and third pure states have probabilities of "q" and "r." Unlike pure states when we measure the state we get one corresponding eigenvalue and we will get the same eigenvalue for infinite times (until the measurement axis is changed), the mixed state if we measure it and find psi_1, the next measurement might yield other states. This probabilistic mixture of pure states is called the mixed states. For a mixed state, the eigenvalues are between 0 and 1.
The sum of the corresponding probabilities in the mixed state should always be 1. (p+q+r=1) .
The Trace of the density squared for a mixed state is always less than 1.
What does the eigenvalue of the state mean in QI?
Eigenvalues are the corresponding values we get after we make a measurement in the quantum state. This means, that whenever we collapse our wavefunction of a given state, the results it yields correspond to the eigenvalue of that state. For a pure state, the eigenvalue is always 1,0,0,..0 which means that whenever we measure a pure state the outcome is always certain which means it only has one corresponding eigenvalue which is embedded in the superposition. For a mixed state, the eigenvalues are between 0 and 1 which means the measurement depends both on probability and superposition. That being said, the outcome of the mixed state is uncertain. Similarly, we can have a condition where the eigenvalues are exactly equal which is 1/2, 1/2, or 1/4,1/4,1/4,1/4. When eigenvalues are equal, then the state is maximally mixed in which the measurement will only depend on probability and the entropy is maximum so there is no superposition embedded in this state which is why we call it the "classical state" since it loses all quantum properties.
3. Maximally Mixed State:
Like mixed states, the maximally mixed states are also the special case for pure states where the state is a statistical mixture of different pure states that depend only on probability. However, the key difference here is that the probability is equally distributed for the corresponding states which means the state is in such a mixture that each outcome is equally probable. For a mixed state, the probability is not equally distributed, meaning the outcome of getting psi_1 could be 90%, while the result of getting psi_2 could be 10%, favoring the first state. However, for a maximally mixed state, the probability for each corresponding state is 50% which means any outcome is equally likely to occur after measurement. This means that the state is now maximally mixed where we truly don't know about the outcome of the state and hence the entropy for this kind of state is maximum.
We generally refer to a maximally mixed state as a classical state since it doesn't acquire any quantum nature, unlike pure and mixed states. Since the state only depends upon the probability, there is no superposition present and it acts completely classical. For a pure state, if after measurement the result is spin down then it doesn't matter how many times we measure the same state we will always get the same spin down (unless we change the measurement axis which means from the z-axis to the x-axis). For a mixed state, there is some quantum magic, even if multiple states are combined with their corresponding probabilities, their randomness is not uniformly distributed which still addresses the superposition property. However, since the probability is equally distributed in a maximally mixed state, the result is always chaos. If we measure the state and find it in spin-up, the second measurement might be either up or down with equal probability.
Bloch Sphere
A Bloch sphere is a representation of the purity of the states. The circumference of the sphere describes the pure state while the origin is the maximally mixed state. Anything between the origin and circumference is a mixed state.
The representation of purity of the states inside a sphere is a very effective way of visualizing the state in quantum information. This method not only explains the purity, but it also has other applications as well such as the geometry of bit flip for pure state or representation of decoherence (converting a pure state to a mixed state).
In quantum mechanics, almost every principle we use such as entanglement, tunneling, or quantum cryptography, we assume the qubit is pure. Since pure states have minimum entropy and their quantum nature is more robust than mixed states, we typically use pure qubits for our theoretical calculations. Of course, obtaining a pure state is highly difficult in the real world since quantum states are highly fragile and sensible under environmental conditions. This property is called decoherence where the quantum property loses its quantum nature from interacting with the environment which means a pure state is slowly converting to a mixed state. It is almost impossible to convert a maximally mixed state to a pure state since it breaks the second law of thermodynamics (reverse entropy).
In the next part, we will discuss one of the most powerful operators in quantum information that can describe all three purity of the state. We will see the properties of the density operator and its significance in the quantum information field.

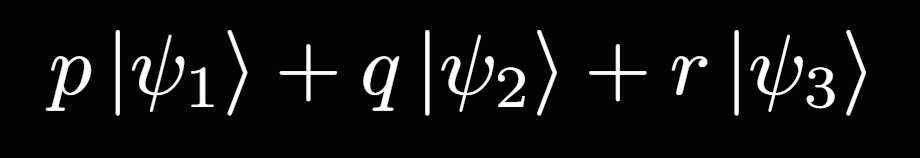


1, 2, 3. The rocket is on🔥
Your comment always means a lot!